السؤالالأول:
( أ ) استخدم عدداً صحيحاً لتمثيل كل موقف مما يأتي :
1) 25° C درجة تحت الصفر …………………………..
2) هبط المصعد ثلاثة أدوار …………………………..
3) ادخرت مبلغ 300 درهما ً …………………………..
( ب ) أكمل ما يأتي :
1) المعكوس الجمعي للعدد الصحيح 14 هو ……………………..
2)
اكتب عددا صحيحا ً يمثل كل نقطة على خط الأعداد التالي :
……….
……….
(ج) رتب درجات الحرارة التالية من الأصغر للأكبر
× درجة حرارة جسم الإنسان الطبيعية 37°C
× درجة الحرارة خارج الطائرة أثناء الرحلة كانت
× أدنى درجة حرارة سُجلت في مدينة لندن
× أعلى درجة حرارة سُجلت في مدينة السلع
الترتيب :
………………………………………….. ………………………………………….. ….
-
 111.doc (381.0 كيلوبايت, 302 مشاهدات)
111.doc (381.0 كيلوبايت, 302 مشاهدات)




 – هي مجموعة جزئية من
– هي مجموعة جزئية من  . وتكون مجموعة الأعداد القياسية
. وتكون مجموعة الأعداد القياسية  و
و متساويان فقط وفقط إذا كان ad = bc.
متساويان فقط وفقط إذا كان ad = bc. وتتم عملية
وتتم عملية 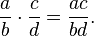 كما يوجد أيضًا المقلوب الجمعي والجدائي في الأعداد الكسرية كما يلي:
كما يوجد أيضًا المقلوب الجمعي والجدائي في الأعداد الكسرية كما يلي:


